Predictive Coding for Locally Linear Control

Problem

With the rapid growth of systems equipped with powerful sensing devices, the ability to control systems from high-dimensional raw sensory inputs (e.g., images) is paramount. More specifically, we can develop intelligent agents that can act in a complex environment to achieve a specific goal, using only a camera sensor without any human supervision. This will enable new advances in many different industries, such as robot manipulation in manufacturing or self-driving cars. For example, we might have a robot which is interacting with the surrounding environment. Everytime the robot moves, it receives an image taken from a camera sensor. Based purely on these data, the robot needs to find an optimal sequence of actions in order to perform a particular task, e.g., pick up an object on the table.

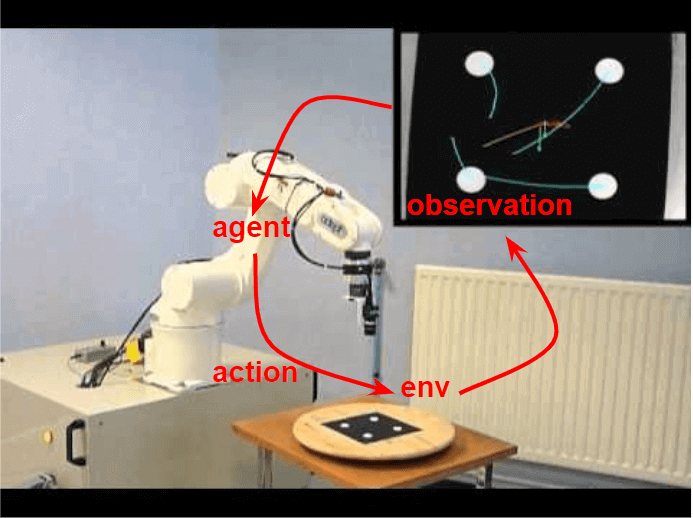
Figure 1. An example of optimal control from pixels.

Related work

A promising approach in solving that problem is the Learning Controllable Embedding (LCE) framework, which embeds the observations into a lower-dimensional latent space, estimates the latent dynamics, and then performs control directly in the latent space.

Figure 2. LCE approach. First, learn the encoder and latent dynamics (left) and then perform control in the latent space (right).

However, the existing LCE-based methods rely on explicit next-observation prediction, which suffers from two critical drawbacks:

• It requires the model to handle the challenging task of high-dimensional prediction.
• It does so in a parameter-inefficient manner—requiring the use of a decoder that is discarded during control.

The proposed method

To address these concerns, we propose a novel information-theoretic LCE approach for learning a controllable latent space (see Figure 3). Unlike previous methods, which explicitly introduce a decoder D and conduct next-observation predictions, we propose to use F as a variational device to train E via predictive coding.

Figure 3. Two high-level approaches to learn encoder E and decoder F.

We show theoretically that predictive coding is a valid alternative to next-observation prediction for learning latent representation. Specifically, we introduce predictive suboptimality, a concept to characterize the suboptimality of next-observation prediction when the prediction model is forced to rely on the learned representation. In doing so, we prove that the predictive suboptimality is upper bounded by the mutual information gap between two consecutive observations and their corresponding latent representations. In other words, by maximizing the mutual information between latent vectors of two consecutive time steps, we can learn a representation that is good for predicting the next observation, without decoding back to the observation space.

Based on this analysis, we identify three desiderata for guiding the selection of the encoder E and latent dynamics model F . We summarize them as follows: (i) predictive coding minimizes the predictive suboptimality of the encoder E; (ii) consistency of the latent dynamics model F enables planning directly in the latent space; and (iii) low-curvature enables planning in latent space specifically using locally-linear controllers. We refer to these heuristics collectively as Predictive Coding-Consistency-Curvature (PC3).

Empirical results

We compare the performance of our proposed model 6 with two state-of-the-art LCE baselines: PCC and SOLAR. The experiments are based on four image-based control benchmark domains: Planar System, Inverted Pendulum, Cartpole, and 3-Link Manipulator.

Table 1. Percentage steps in goal state for the average model (all) and top 1 model.

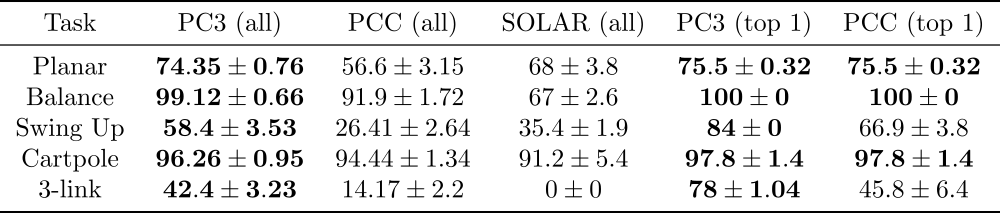
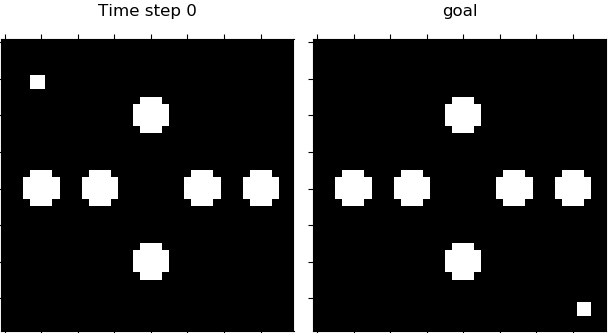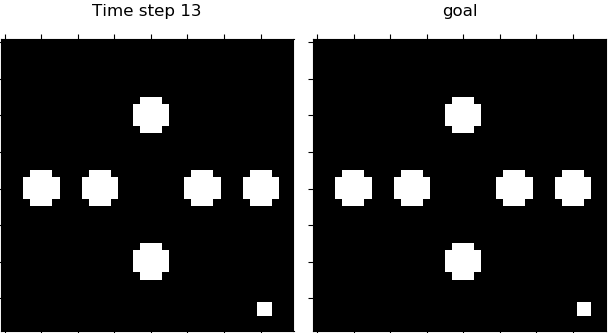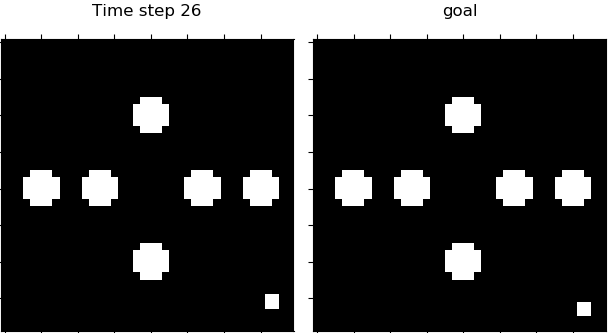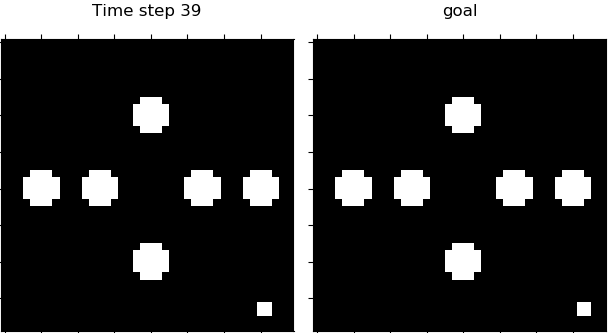
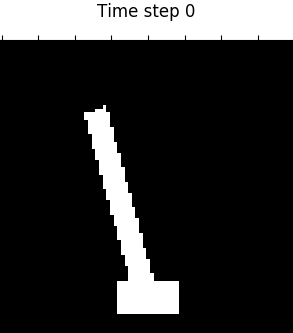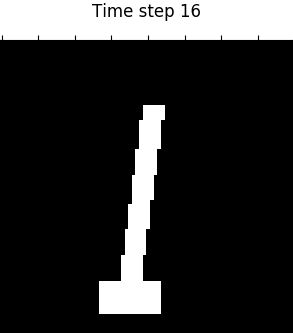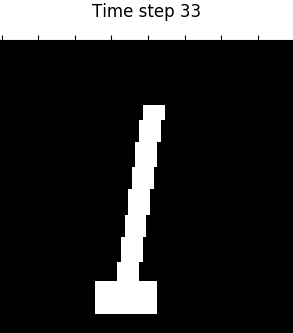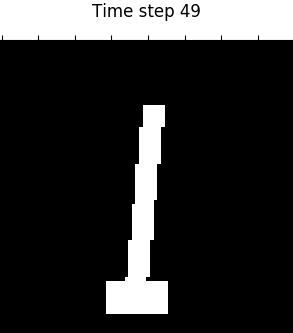
Figure 4. Visualization of 4 domains during control. From left to right: Planar, Inverted Pendulum, Cartpole, 3-Link Manipulator.

Table 1 shows that our proposed PC3 model significantly outperforms the baselines by comparing the means and standard error of means on the different control tasks. Figure 4 demonstrates some latent maps of Inverted Pendulum domain learned by PCC and PC3. In general, PC3 produces more interpretable latent representations, due to the fact that next observation prediction is too conservative and may force a model to care about things that do not matter to downstream tasks.

Figure 5. Left two: PCC, right two: PC3. Each color represents an angle, and different points of the same color represent different angular velocities.

Figure 6. Visualization of latent maps during training. Left: Planar, right: Inverted Pendulum.